12 Out Of 16 Percentage
braininterpreter
Sep 23, 2025 · 5 min read
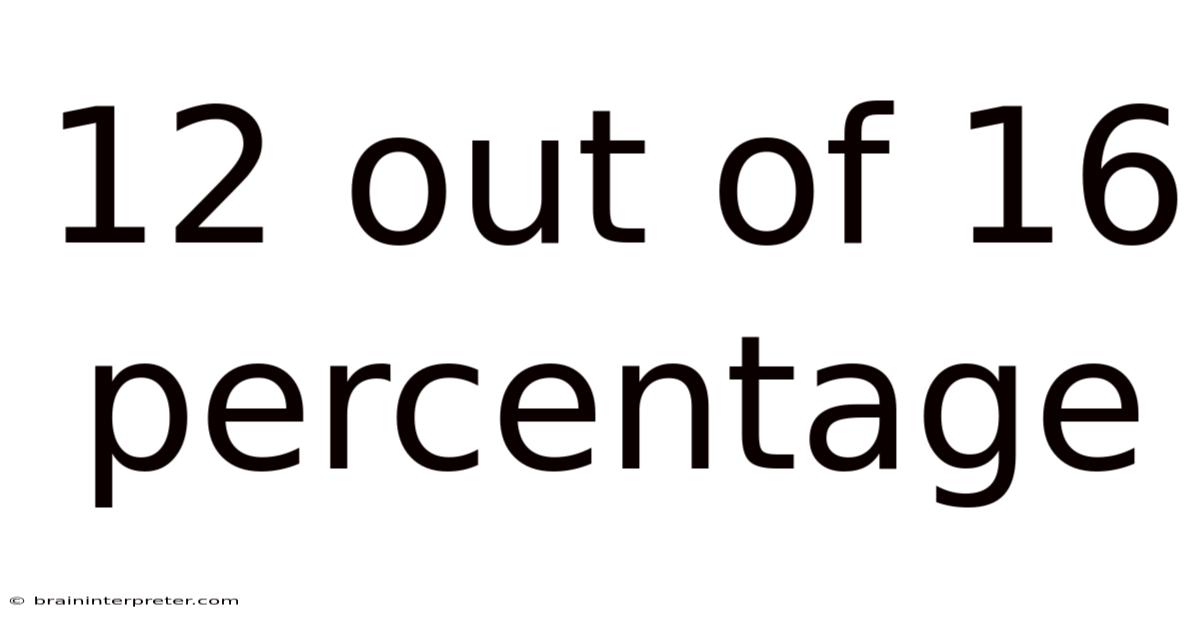
Table of Contents
Understanding 12 out of 16: A Comprehensive Guide to Percentages and Fractions
Calculating percentages is a fundamental skill applicable in numerous areas of life, from academic assessments to financial planning. This article will delve into the specifics of calculating and understanding what 12 out of 16 represents as a percentage, providing a detailed explanation accessible to all levels of understanding. We'll explore the underlying principles of fractions, percentages, and ratios, offering practical examples and addressing frequently asked questions. This comprehensive guide will equip you with the tools to confidently tackle similar percentage calculations in the future.
Understanding Fractions and Ratios
Before diving into percentages, it's crucial to grasp the concepts of fractions and ratios. A fraction represents a part of a whole. In the case of "12 out of 16," the fraction is expressed as 12/16. The top number (12) is the numerator, representing the part, and the bottom number (16) is the denominator, representing the whole.
A ratio compares two or more quantities. The ratio of 12 to 16 can be written as 12:16. Both fractions and ratios provide a way to express the relationship between two numbers. Understanding these concepts is essential for calculating percentages effectively.
Calculating the Percentage: Step-by-Step
Converting a fraction to a percentage involves a straightforward process:
-
Simplify the Fraction: The first step is to simplify the fraction 12/16. Both the numerator and the denominator share a common factor of 4. Dividing both by 4, we get the simplified fraction 3/4. Simplifying fractions makes the subsequent calculations easier.
-
Convert to a Decimal: To convert the simplified fraction 3/4 to a decimal, divide the numerator (3) by the denominator (4). This gives us 0.75.
-
Convert to a Percentage: To express the decimal as a percentage, multiply the decimal by 100 and add the percent symbol (%). So, 0.75 multiplied by 100 equals 75%.
Therefore, 12 out of 16 is equivalent to 75%.
Visualizing the Percentage
Visual aids can significantly enhance the understanding of percentages. Imagine a pie chart divided into 16 equal slices. If 12 slices are shaded, it represents 75% of the entire pie. This visual representation makes the concept more intuitive and easily grasped. Similarly, a bar graph could be used, where 75% of the bar is filled to represent 12 out of 16.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in many real-world situations. Here are some examples:
-
Academic Performance: If a student answers 12 out of 16 questions correctly on a test, their score is 75%. This helps determine their grade and overall academic standing.
-
Financial Calculations: Percentages are fundamental in calculating interest rates, discounts, tax rates, and profit margins. Understanding these calculations helps in making informed financial decisions.
-
Data Analysis: Percentages are extensively used to represent and interpret data in various fields, including market research, scientific studies, and business analytics. They simplify the understanding of complex datasets.
-
Everyday Life: Percentages are encountered in everyday scenarios, such as calculating tips, sales tax, or discounts at stores.
Different Methods for Calculating Percentages
While the step-by-step method outlined above is straightforward, there are other approaches to calculate percentages. These alternative methods can be useful depending on the context and the complexity of the calculation.
-
Using Proportions: This method involves setting up a proportion to solve for the unknown percentage. For instance, you could set up the proportion: 12/16 = x/100, where x represents the percentage. Solving for x will give you the percentage.
-
Using a Calculator: Most calculators have a percentage function that simplifies the calculation. Simply enter 12 divided by 16 and then multiply by 100 to get the percentage.
-
Using Spreadsheet Software: Spreadsheet software like Microsoft Excel or Google Sheets provides built-in functions for calculating percentages, making the process efficient and accurate.
Understanding Percentage Increase and Decrease
The concept of percentage can also be applied to understand changes in quantities over time. Let's say a quantity increases from 16 to 20. The percentage increase is calculated as follows:
- Find the difference: 20 - 16 = 4
- Divide the difference by the original value: 4 / 16 = 0.25
- Multiply by 100 to get the percentage: 0.25 * 100 = 25%
Therefore, there is a 25% increase from 16 to 20. Similarly, you can calculate percentage decrease using the same principles.
Addressing Common Misconceptions about Percentages
Several common misconceptions surround percentages, and understanding these is important for accurate calculations:
-
Adding Percentages Directly: It's incorrect to add percentages directly without considering the base values. For example, a 10% increase followed by a 10% decrease does not result in the original value; it results in a slight decrease.
-
Confusing Percentages with Absolute Values: Percentages represent a proportion of a whole, not an absolute value. A large percentage of a small number might be less than a small percentage of a large number.
-
Incorrectly Interpreting Percentage Changes: Always clearly state the base value when discussing percentage changes to avoid ambiguity.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of the fraction 12/16?
- A: The simplest form of the fraction 12/16 is 3/4.
-
Q: How can I calculate percentages without a calculator?
- A: You can calculate percentages manually by following the step-by-step method outlined earlier: simplify the fraction, convert to a decimal by dividing the numerator by the denominator, and then multiply by 100 to get the percentage.
-
Q: What if I have a more complex fraction?
- A: The same principles apply to more complex fractions. Simplify the fraction first, then convert to a decimal, and finally multiply by 100 to get the percentage.
-
Q: How are percentages used in real-world applications?
- A: Percentages are used extensively in finance, academics, data analysis, and everyday life for calculating various proportions, changes, and comparisons.
Conclusion
Understanding how to calculate and interpret percentages is a crucial skill with widespread applications. This comprehensive guide has provided a detailed explanation of calculating 12 out of 16 as a percentage (75%), including step-by-step instructions, visual aids, and practical examples. By mastering these concepts, you will be better equipped to handle percentage calculations in various aspects of your life, making informed decisions based on accurate numerical representation. Remember to always pay attention to the underlying principles of fractions and ratios, and avoid common misconceptions to ensure accurate calculations and interpretations.
Latest Posts
Latest Posts
-
Convert M3 To Cubic Feet
Sep 23, 2025
-
How High Is 60 Feet
Sep 23, 2025
-
600 Ml Water To Cups
Sep 23, 2025
-
20 Percent Of 20 Million
Sep 23, 2025
-
Whats 49 Inches In Feet
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 12 Out Of 16 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.