26 Out Of 30 Percentage
braininterpreter
Sep 22, 2025 · 5 min read
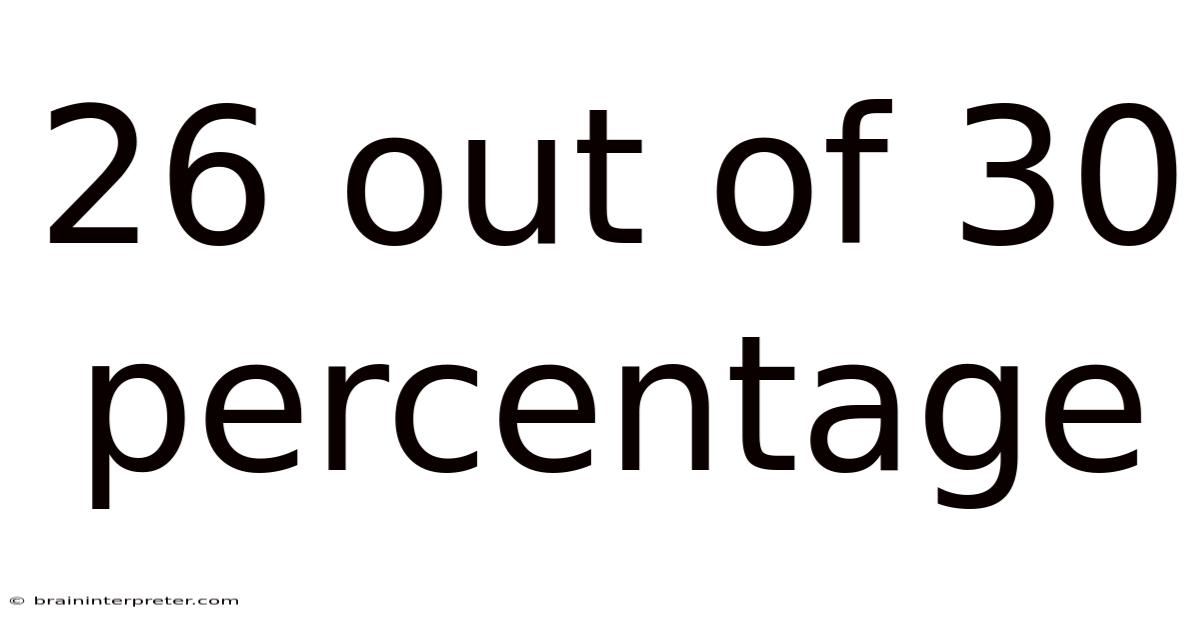
Table of Contents
Understanding 26 out of 30: Percentage, Fraction, and Real-World Applications
Obtaining a score of 26 out of 30 on a test, assignment, or any graded assessment is a significant achievement. This article will delve into the various ways to interpret this score, exploring its representation as a percentage, fraction, and demonstrating its relevance in different real-world scenarios. We'll also unpack the underlying mathematical concepts and address frequently asked questions to provide a comprehensive understanding of this seemingly simple yet insightful numerical result.
Understanding Percentage Calculations
The most common way to interpret 26 out of 30 is as a percentage. A percentage represents a portion of a whole, expressed as a fraction of 100. To calculate the percentage, we use the following formula:
(Part / Whole) * 100%
In this case, the part is 26 (the score achieved), and the whole is 30 (the total possible score). Therefore, the calculation is:
(26 / 30) * 100% = 86.67%
This means a score of 26 out of 30 represents 86.67%. This is a high score, indicating a strong performance.
Representing the Score as a Fraction
Alternatively, the score can be represented as a fraction. A fraction shows the relationship between two numbers, representing a part of a whole. In this instance, the fraction is:
26/30
This fraction can be simplified by finding the greatest common divisor (GCD) of 26 and 30, which is 2. Dividing both the numerator and denominator by 2, we get:
13/15
Both 26/30 and 13/15 represent the same proportion of the total score, just expressed differently. The simplified fraction, 13/15, provides a more concise representation.
Real-World Applications and Interpretations
The significance of a 26 out of 30 score varies depending on the context. Here are some examples:
-
Academic Assessments: In an academic setting, 86.67% is generally considered a very good grade, often falling within the A or A- range depending on the grading scale used by the institution. It indicates a strong understanding of the subject matter.
-
Competitive Examinations: In competitive exams, the interpretation changes. While 86.67% is a good score, its significance depends on the overall performance of other candidates. A percentile rank, which indicates the percentage of candidates scoring below a particular score, provides a more accurate picture of relative performance.
-
Performance Evaluations: In professional settings, a 26 out of 30 score on a performance review might represent excellent performance in a specific task or area. However, the overall performance evaluation usually depends on multiple factors, not solely on this particular score.
-
Statistical Analysis: In statistical contexts, 26 out of 30 could represent data related to surveys, experiments, or quality control. It might show the success rate of a process or the proportion of respondents who agree with a particular statement. Further statistical analysis, such as calculating confidence intervals, could provide more insights into the significance of this data point.
Mathematical Concepts and Further Exploration
Understanding the concepts behind percentages and fractions is crucial. Here's a deeper dive:
-
Percentages: Percentages are used extensively to represent proportions, rates, and changes in various fields, including finance, economics, and science. Understanding percentage calculations is essential for interpreting data, making informed decisions, and communicating effectively.
-
Fractions: Fractions form the foundation of arithmetic and algebra. They represent parts of a whole and are fundamental to understanding ratios, proportions, and other mathematical concepts. Simplifying fractions is crucial for easier calculations and clearer representations.
-
Ratios: The score of 26 out of 30 can also be expressed as a ratio: 26:30 or, simplified, 13:15. Ratios express the quantitative relationship between two or more amounts. They are often used in recipes, map scales, and comparing different quantities.
-
Proportions: A proportion is a statement of equality between two ratios. For instance, the proportion 26/30 = x/100 is used to calculate the percentage. Understanding proportions is vital for solving many real-world problems involving scaling, scaling down, and comparing ratios.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate the percentage from a fraction?
- A: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100%. For example, (26/30) * 100% = 86.67%
-
Q: What if the total possible score is different? How does the calculation change?
- A: The calculation remains the same: (Part / Whole) * 100%. Just replace the 'Whole' with the new total possible score.
-
Q: How can I improve my understanding of percentages and fractions?
- A: Practice is key! Try solving various problems involving percentages and fractions, and utilize online resources or textbooks for further learning and clarification.
-
Q: What's the difference between a percentage and a percentile?
- A: A percentage represents a proportion of a whole. A percentile, on the other hand, indicates the rank of a score relative to other scores in a dataset. For instance, being in the 86th percentile means scoring higher than 86% of the other test takers.
-
Q: Is there a way to calculate the percentage without a calculator?
- A: For simple calculations, you can perform long division. For more complex calculations, you can utilize estimation techniques or refer to percentage charts.
Conclusion
A score of 26 out of 30, representing 86.67% or 13/15, signifies a strong performance across various contexts. Understanding how to calculate this score as a percentage and a fraction, and interpreting its significance in different situations is crucial. The underlying mathematical concepts of percentages, fractions, ratios, and proportions are essential tools in understanding and interpreting numerical data in our daily lives. This detailed explanation provides a solid foundation for appreciating the value and implications of this seemingly simple numerical result, highlighting its versatility and importance in various academic, professional, and statistical applications. Remember to practice calculating percentages and fractions regularly to enhance your understanding and problem-solving skills. The more you practice, the more confident you'll become in tackling similar numerical challenges in the future.
Latest Posts
Latest Posts
-
How Many Centimeters Is 4 10
Sep 23, 2025
-
Yards To Square Meters Conversion
Sep 23, 2025
-
60 Days From January 29th
Sep 23, 2025
-
How Long Is 15 M
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 26 Out Of 30 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.