5 Out Of 7 Percentage
braininterpreter
Sep 15, 2025 · 6 min read
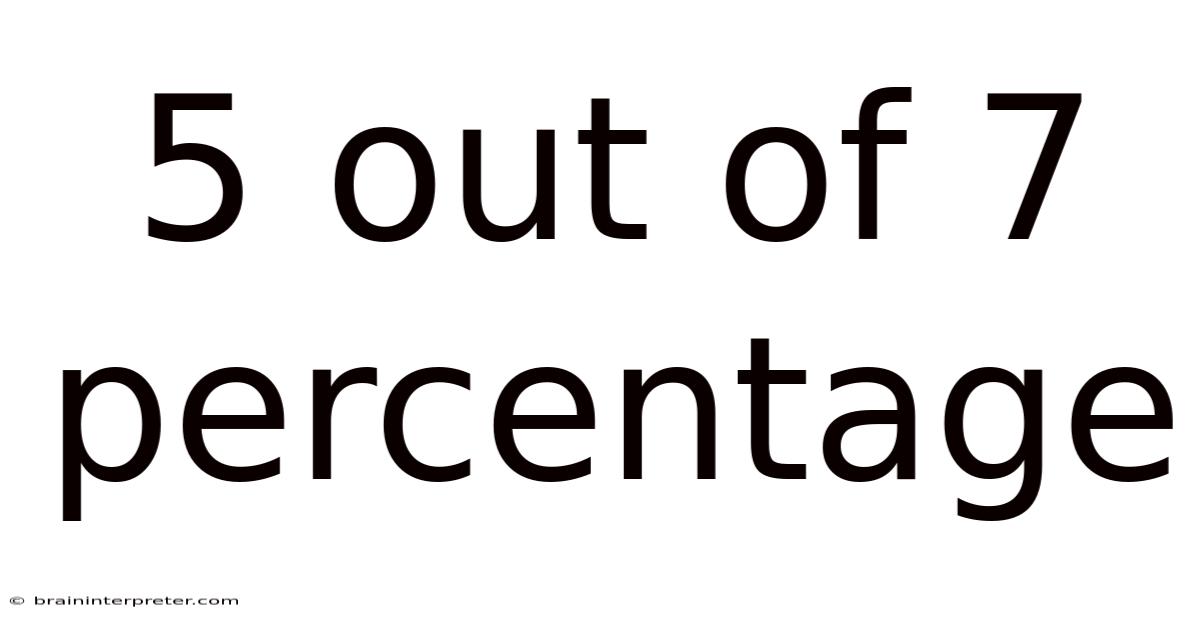
Table of Contents
Decoding the "5 out of 7": Understanding Percentages and Proportions
Understanding percentages is a fundamental skill in everyday life, from calculating discounts and taxes to interpreting statistics and analyzing data. This article delves deep into the seemingly simple concept of "5 out of 7," explaining not only its percentage equivalent but also the underlying principles of proportions and their applications in various fields. We'll explore how to calculate this percentage, its practical implications, and address common misconceptions. This comprehensive guide will equip you with the knowledge to confidently tackle similar percentage problems.
Introduction: What Does "5 out of 7" Mean?
The phrase "5 out of 7" represents a proportion—a comparison of two quantities. It tells us that out of a total of 7 items or events, 5 possess a specific characteristic. To understand its meaning fully, we need to translate this proportion into a percentage, a standardized way of expressing parts of a whole as a fraction of 100.
Calculating the Percentage: A Step-by-Step Guide
Calculating the percentage represented by "5 out of 7" involves a straightforward process:
-
Express the proportion as a fraction: "5 out of 7" can be written as the fraction 5/7.
-
Convert the fraction to a decimal: Divide the numerator (5) by the denominator (7): 5 ÷ 7 ≈ 0.7143
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percent sign (%): 0.7143 × 100 ≈ 71.43%
Therefore, 5 out of 7 represents approximately 71.43%.
Understanding Proportions and Ratios
The concept of "5 out of 7" is inherently linked to proportions and ratios. A ratio compares two quantities, while a proportion states that two ratios are equal. In our case, the ratio is 5:7 (5 to 7), and a proportion might compare this ratio to another, such as the ratio of a larger sample. For instance, if a larger sample of 14 items contains 10 with the same characteristic, then the proportion 5:7 = 10:14 holds true. Understanding proportions is crucial in various fields like:
- Business and Finance: Calculating profit margins, market share, and investment returns.
- Science: Determining experimental success rates, analyzing data, and modeling relationships between variables.
- Everyday Life: Understanding discounts, sales tax, and recipe adjustments.
Real-World Applications of Percentage Calculations
Let's explore some real-world scenarios where understanding "5 out of 7" (or similar percentage calculations) is essential:
-
Test Scores: If a student answers 5 out of 7 questions correctly on a quiz, their score is approximately 71.43%. This allows for easy comparison of performance across different tests and students.
-
Survey Results: If a survey of 7 people reveals that 5 prefer a particular brand, the brand has approximately 71.43% preference among those surveyed. This is a simple example; larger sample sizes are crucial for accurate statistical inferences.
-
Manufacturing Quality Control: If a batch of 7 products contains 5 defects, the defect rate is approximately 71.43%. This high rate indicates a significant problem requiring immediate attention in the manufacturing process.
-
Medical Trials: If 5 out of 7 patients respond positively to a new treatment, the success rate is approximately 71.43%. This is a preliminary finding that would require further, more extensive testing to validate.
-
Sports Statistics: A basketball player making 5 out of 7 free throws has a free-throw percentage of approximately 71.43%. This statistic helps evaluate the player's performance and consistency.
Beyond the Calculation: Interpreting the Results
While the calculation of 71.43% is straightforward, correctly interpreting the results within the context of the problem is crucial. For example:
-
Sample Size Matters: A 71.43% success rate based on a sample size of 7 is less reliable than the same percentage based on a sample size of 700. Larger sample sizes provide greater statistical confidence.
-
Context is Key: The meaning of 71.43% depends entirely on the context. A 71.43% success rate in a medical trial has significantly different implications than a 71.43% customer satisfaction rating.
Advanced Concepts: Error and Uncertainty
It's important to remember that the percentage calculated (71.43%) is an approximation. The decimal representation (0.7143) continues infinitely, implying an inherent level of uncertainty. This uncertainty is amplified when working with smaller sample sizes. In statistical analysis, methods exist to quantify and account for this uncertainty, providing a measure of confidence in the calculated percentage. These methods are beyond the scope of this introductory article, but it's essential to understand that absolute precision is often unattainable, especially when dealing with real-world data.
Addressing Common Misconceptions
Some common misconceptions regarding percentages include:
-
Confusing percentages with proportions: While related, percentages represent parts of a whole as a fraction of 100, while proportions compare two quantities directly.
-
Incorrect rounding: Rounding errors can accumulate and lead to inaccurate results. It's important to maintain sufficient decimal places during calculations and only round the final answer appropriately.
-
Ignoring sample size: The reliability of a percentage heavily depends on the sample size. Small samples can lead to misleading results.
-
Assuming causality: A high percentage doesn't automatically imply causality. Correlation doesn't equal causation. For instance, a high percentage of people who own cats also own dogs doesn't mean cat ownership causes dog ownership.
Frequently Asked Questions (FAQ)
-
Q: How can I calculate percentages quickly without a calculator?
- A: For simple percentages, you can use mental math techniques. For example, 10% is found by dividing by 10, 50% by dividing by 2, etc. You can combine these techniques to calculate more complex percentages.
-
Q: What if the number of items isn't a whole number?
- A: The same principles apply. You can still express the proportion as a fraction and convert it to a percentage using division and multiplication.
-
Q: How do I deal with percentages greater than 100%?
- A: Percentages greater than 100% represent values larger than the whole. This is perfectly valid in certain contexts, such as when comparing growth or increase.
-
Q: Are there any online tools or calculators for percentage calculations?
- A: Yes, numerous online calculators and tools can perform percentage calculations quickly and accurately.
Conclusion: Mastering Percentages – A Foundation for Success
Understanding "5 out of 7" – and the broader concept of percentages – is a crucial skill applicable across many disciplines. This article has not only demonstrated how to calculate this specific percentage but has also explored the underlying principles of proportions, ratios, and the importance of context and sample size in interpreting the results. By mastering these concepts, you'll be well-equipped to tackle a wide range of percentage-related problems with confidence, improving your analytical skills and enhancing your understanding of the world around you. Remember, the key is not just to calculate the percentage but to interpret its meaning correctly within the given context.
Latest Posts
Latest Posts
-
2000mg Equals How Many Grams
Sep 15, 2025
-
18 Time And A Half
Sep 15, 2025
-
How Much Is 85 Kilograms
Sep 15, 2025
-
Tons To Cubic Yards Conversion
Sep 15, 2025
-
6 Inches In A Foot
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 5 Out Of 7 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.