6 Out Of 8 Percentage
braininterpreter
Sep 14, 2025 · 5 min read
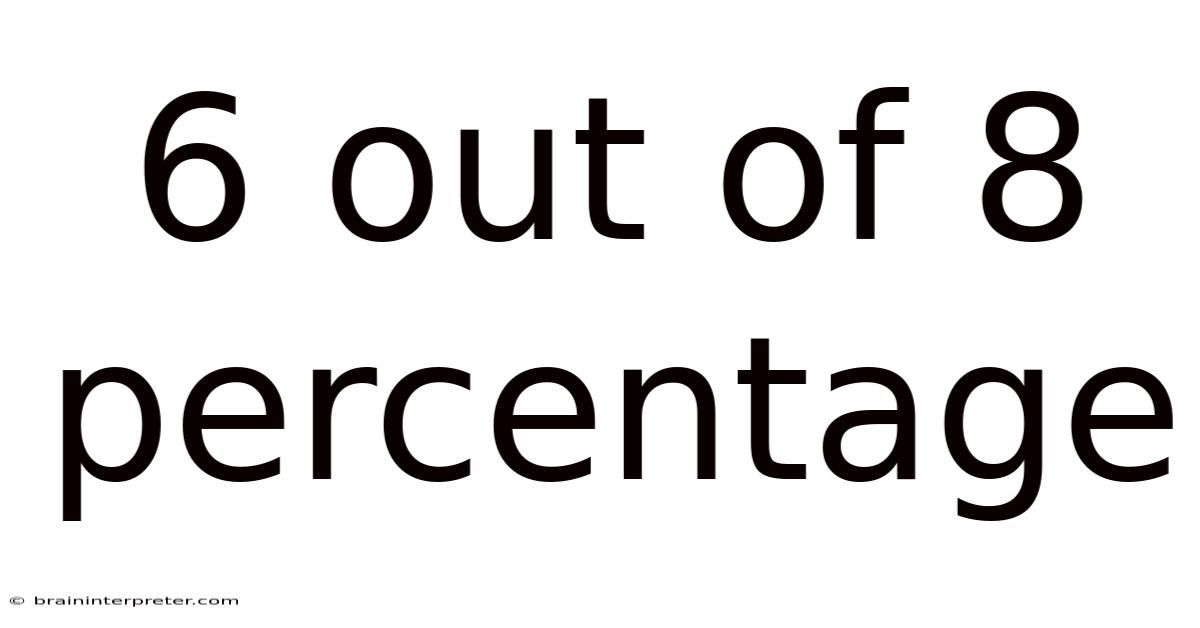
Table of Contents
Understanding 6 out of 8: Fractions, Percentages, and Real-World Applications
Understanding fractions and percentages is a fundamental skill applicable across numerous fields, from basic arithmetic to advanced financial modeling. This article delves into the meaning of "6 out of 8," explaining its representation as a fraction, converting it to a percentage, and exploring its practical applications in everyday life and various professional contexts. We'll also cover common misunderstandings and provide a comprehensive guide to ensure a solid grasp of this concept.
What Does "6 out of 8" Mean?
The phrase "6 out of 8" signifies a ratio or a fraction. It means that out of a total of 8 items or units, 6 possess a specific characteristic or meet a certain criterion. This can be anything from 6 correct answers out of 8 questions on a quiz to 6 sunny days out of a total of 8 days in a week.
Representing "6 out of 8" as a Fraction
Mathematically, "6 out of 8" is represented as a fraction: 6/8. The numerator (6) represents the part, and the denominator (8) represents the whole. This fraction can be simplified by finding the greatest common divisor (GCD) of both the numerator and the denominator. The GCD of 6 and 8 is 2. Dividing both the numerator and the denominator by 2 simplifies the fraction to its lowest terms: 3/4. Therefore, "6 out of 8" is equivalent to 3/4.
Converting the Fraction to a Percentage
To express "6 out of 8" as a percentage, we need to convert the fraction 3/4 (or 6/8) into a percentage. A percentage is a fraction expressed as a number out of 100. We can do this by performing the following calculation:
(3/4) * 100% = 75%
Therefore, "6 out of 8" is equivalent to 75%.
Real-World Applications of "6 out of 8" and 75%
The concept of "6 out of 8" and its equivalent 75% is frequently encountered in various scenarios:
-
Academic Performance: A student scoring 6 out of 8 on a test achieved a grade of 75%. This helps in understanding their performance relative to the total marks.
-
Business and Finance: In sales, if a salesperson achieved 6 sales out of 8 potential clients, their success rate is 75%. This metric is crucial for performance evaluation and strategic planning. Similarly, in market research, 75% market share indicates a dominant position. Financial analysis often involves calculating percentages of income, expenses, profits, and losses.
-
Surveys and Polls: If 6 out of 8 respondents agreed with a particular statement in a survey, this translates to a 75% agreement rate. This data is valuable in understanding public opinion and consumer preferences.
-
Project Management: If a project consists of 8 tasks and 6 are completed, the project's completion rate is 75%. This metric helps track progress and identify potential delays.
-
Sports Statistics: A basketball player making 6 out of 8 free throws has a 75% free-throw percentage. This statistic is essential for assessing a player's performance.
-
Manufacturing and Quality Control: In a manufacturing process, if 6 out of 8 products pass quality checks, the yield rate is 75%. This informs decisions regarding production efficiency and defect reduction.
-
Medical Studies and Research: In clinical trials, the success rate of a treatment can be expressed as a percentage. For example, if 6 out of 8 patients showed improvement, the success rate would be 75%.
-
Everyday Life: Numerous situations in daily life involve fractions and percentages. For example, if you eat 6 slices out of an 8-slice pizza, you consumed 75% of the pizza.
Understanding the Concept of Proportions
The concept of "6 out of 8" is intrinsically linked to proportions. A proportion is a statement that two ratios are equal. We can express this as:
6/8 = x/100
Solving for x, we get:
x = (6/8) * 100 = 75
This shows that the ratio 6/8 is equivalent to the ratio 75/100, which represents 75%.
Common Misunderstandings and Errors
While the concept seems straightforward, some common misunderstandings can lead to errors:
-
Incorrect Simplification of Fractions: Failing to simplify fractions to their lowest terms can lead to inaccurate calculations and comparisons.
-
Confusion between Fractions and Percentages: Not understanding the relationship between fractions and percentages can result in incorrect conversions.
-
Incorrect application of percentages: Misinterpreting percentage increases or decreases, especially in compound interest calculations, is a common pitfall.
-
Ignoring the context: Misinterpreting the significance of a percentage without considering the context of the data. For example, a 75% success rate in a small sample size might not be as significant as a 75% success rate in a large sample size.
Frequently Asked Questions (FAQs)
Q1: How do I calculate a percentage increase or decrease?
To calculate a percentage increase or decrease, find the difference between the new value and the original value. Then, divide this difference by the original value and multiply by 100%. For example: if the original value is 8 and the new value is 10, the percentage increase is ((10-8)/8)*100% = 25%.
Q2: What are some common uses of percentages in daily life?
Percentages are used to express sales tax, discounts, tips, interest rates, inflation rates, and many other financial calculations. They also frequently appear in news reports, expressing data related to unemployment rates, election results, and economic growth.
Q3: How can I improve my understanding of fractions and percentages?
Practice is key. Work through various examples, solve problems, and use online resources and educational materials to reinforce your understanding.
Conclusion: Mastering Fractions and Percentages
Understanding the concept of "6 out of 8" and its representation as a fraction (3/4) and percentage (75%) is crucial for navigating various aspects of life and work. Mastering this fundamental concept opens doors to understanding more complex mathematical concepts and applying them effectively in different fields. By understanding the principles, practicing conversions, and being mindful of potential pitfalls, you can confidently utilize fractions and percentages in any situation demanding these skills. The ability to confidently work with percentages provides a significant advantage in academic, professional, and personal settings. So, embrace the challenge, practice diligently, and watch your understanding flourish!
Latest Posts
Latest Posts
-
Convert 160 Cm Into Feet
Sep 14, 2025
-
Sticks Of Butter To Pounds
Sep 14, 2025
-
90 Days From 12 5
Sep 14, 2025
-
45 Days From August 26
Sep 14, 2025
-
How Many Minutes Is 120
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 6 Out Of 8 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.