8 Billion Times 1 Million
braininterpreter
Sep 15, 2025 · 5 min read
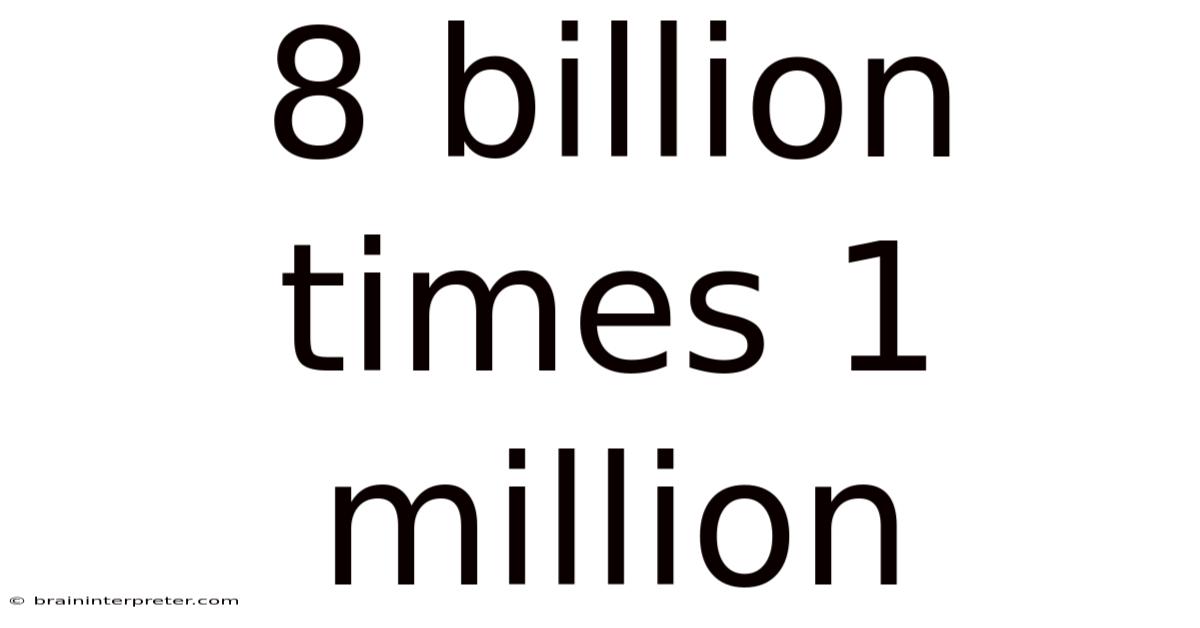
Table of Contents
8 Billion Times 1 Million: Unpacking a Gigantic Number
What happens when you multiply 8 billion by 1 million? The result is a number so vast it's difficult to truly comprehend. This article will delve into the calculation, explore the magnitude of the final figure, and provide relatable examples to help grasp its sheer scale. We'll also discuss the mathematical concepts involved and explore some practical applications where understanding such large numbers is crucial. This exploration aims to demystify this seemingly daunting calculation and reveal the fascinating world of extremely large numbers.
Understanding the Calculation: 8 Billion x 1 Million
Let's start with the basics. 8 billion can be written as 8,000,000,000, and 1 million as 1,000,000. Multiplying these two numbers gives us:
8,000,000,000 x 1,000,000 = 8,000,000,000,000,000
This is eight quintillion. In scientific notation, this is 8 x 10<sup>18</sup>. But what does this number actually mean? It's a number so large that it's beyond our everyday experiences. We struggle to visualize quantities of this magnitude.
The Immensity of Eight Quintillion: Finding Relatable Examples
To make eight quintillion more tangible, let's consider some relatable examples:
-
Grains of Sand: Estimating the number of grains of sand on all the beaches on Earth is a common thought experiment. While precise figures are impossible, estimates often land in the quadrillions (10<sup>15</sup>). Eight quintillion is significantly larger, meaning there are far more than eight thousand times the number of grains of sand on Earth's beaches to equal this amount.
-
Stars in the Observable Universe: The observable universe is estimated to contain hundreds of billions of galaxies, each containing billions of stars. Even with such vast numbers, eight quintillion dwarfs the estimated number of stars in the observable universe. We are talking about many orders of magnitude more.
-
Seconds in a Very Long Time: Let's consider the number of seconds in a million years. There are approximately 31,536,000 seconds in a year (accounting for leap years). In a million years, that's 31,536,000,000,000 seconds. Eight quintillion is still significantly larger, representing roughly 250 million years worth of seconds.
-
Atoms in a Small Object: Even looking at the atomic level doesn't fully capture the scale. While a single grain of sand contains a vast number of atoms, eight quintillion is a number that surpasses the number of atoms in incredibly large objects.
These examples illustrate the sheer incomprehensibility of eight quintillion. It's a number so large that it exceeds readily available analogies.
Mathematical Concepts at Play
The calculation itself involves straightforward multiplication, but understanding the resulting number requires a grasp of:
-
Powers of Ten: The number 8,000,000,000,000,000 can be easily represented using powers of ten (10<sup>18</sup>). This simplifies large number representation and manipulation.
-
Scientific Notation: Scientific notation (8 x 10<sup>18</sup>) provides a concise and efficient way to represent extremely large or extremely small numbers. This is essential in fields like science and engineering where such numbers frequently arise.
-
Orders of Magnitude: Understanding orders of magnitude helps in comparing the relative sizes of numbers. Eight quintillion is many orders of magnitude larger than familiar numbers, emphasizing its colossal size.
Practical Applications of Understanding Large Numbers
While eight quintillion may seem abstract, understanding such large numbers is vital in several fields:
-
Astronomy: Dealing with distances, masses, and the sheer number of celestial bodies requires working with numbers that are many orders of magnitude larger than what we encounter in everyday life.
-
Computer Science: Data storage and processing involve dealing with massive datasets. Understanding the size and scale of data is crucial for efficient management and analysis.
-
Finance: National debts, global markets, and economic forecasts all involve manipulating numbers in the billions and trillions. Understanding these magnitudes is vital for making informed decisions.
-
Physics: In fields like particle physics, numbers representing the quantity of particles or energy levels are often astronomically large.
-
Big Data Analysis: With the increasing availability of large datasets, the ability to process and interpret these immense quantities of information is becoming increasingly critical across various industries.
Frequently Asked Questions (FAQs)
-
Q: How many zeros are in eight quintillion?
A: Eight quintillion has 18 zeros (8,000,000,000,000,000).
-
Q: Can I visualize eight quintillion in any concrete way?
A: It's difficult to visualize such a large number directly. Relatable examples, such as the number of grains of sand on Earth (a far smaller number), are often used to give a sense of scale, but even these fall short of capturing the true immensity.
-
Q: What are some other ways to represent eight quintillion?
A: Besides scientific notation (8 x 10<sup>18</sup>), it can be expressed in different number systems (though the representation will remain just as unwieldy) or by using analogies (as discussed above).
-
Q: Why is it important to understand numbers this large?
A: Understanding large numbers is crucial for comprehending complex systems, making informed decisions in various fields, and appreciating the scale of the universe and the data we interact with daily.
Conclusion: Beyond Comprehension, Yet Within Our Grasp
Eight billion times one million results in eight quintillion – a number so vast it challenges our ability to visualize it directly. However, by employing techniques like scientific notation, exploring relatable analogies, and understanding the underlying mathematical principles, we can begin to grasp the sheer magnitude of such numbers. While fully visualizing eight quintillion remains a challenge, recognizing its scale and understanding its significance in various fields enhances our understanding of the world around us, from the infinitesimally small to the astronomically large. The ability to comprehend and work with such immense quantities is not just a mathematical skill but a vital tool for navigating an increasingly complex and data-driven world. This exploration highlights the importance of developing numerical fluency to tackle challenges across numerous disciplines.
Latest Posts
Latest Posts
-
30 Days From Feb 7
Sep 15, 2025
-
1 57 M Height In Feet
Sep 15, 2025
-
84 Kg How Many Pounds
Sep 15, 2025
-
640 Fl Oz To Gallon
Sep 15, 2025
-
450 Grams In Cups Flour
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 8 Billion Times 1 Million . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.