9 Out Of 14 Percentage
braininterpreter
Sep 17, 2025 · 5 min read
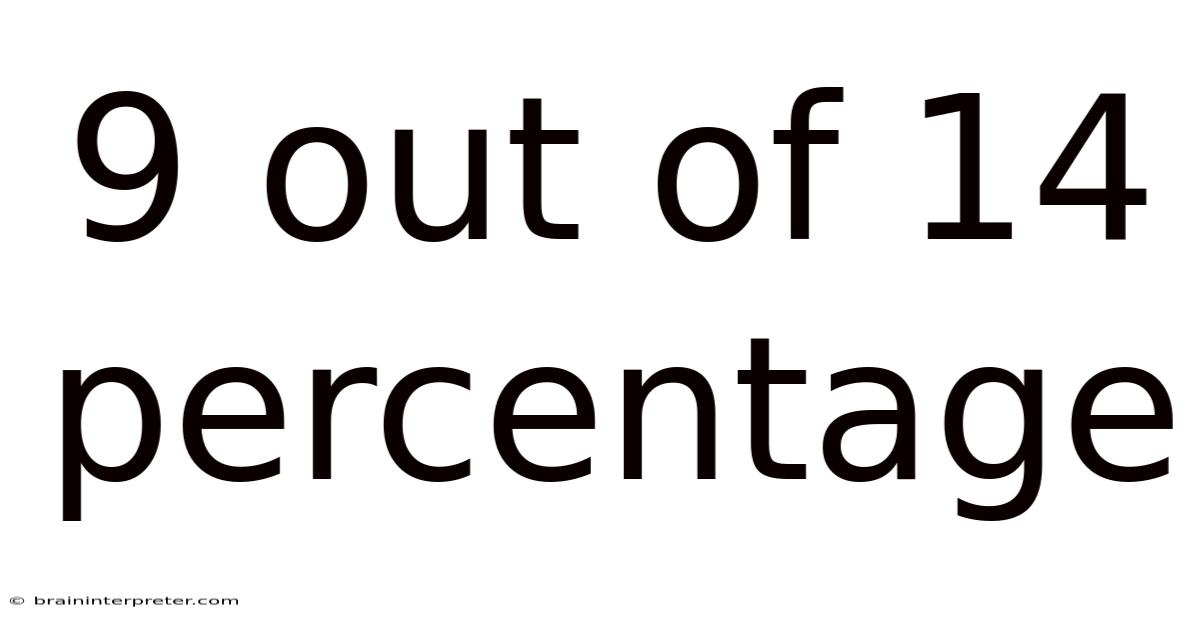
Table of Contents
Decoding 9 out of 14: A Comprehensive Guide to Percentages and Ratios
Understanding percentages and ratios is fundamental to numerous aspects of life, from calculating grades and discounts to comprehending financial reports and statistical analyses. This article delves into the meaning of "9 out of 14," explaining how to calculate its percentage equivalent, exploring its broader implications within the context of ratios and proportions, and addressing common misconceptions. We'll also look at how this seemingly simple calculation applies to various real-world scenarios. This in-depth guide will equip you with a strong grasp of this essential mathematical concept.
What Does "9 out of 14" Mean?
The phrase "9 out of 14" represents a ratio; it signifies that 9 items possess a particular characteristic out of a total of 14 items. This ratio can be expressed in several ways:
- Fraction: 9/14
- Decimal: Approximately 0.643
- Percentage: Approximately 64.3%
Understanding these different representations is crucial for interpreting data and solving problems effectively.
Calculating the Percentage: A Step-by-Step Guide
Converting a ratio to a percentage involves a straightforward process:
-
Express the ratio as a fraction: As mentioned above, "9 out of 14" is expressed as 9/14.
-
Convert the fraction to a decimal: Divide the numerator (9) by the denominator (14). 9 ÷ 14 ≈ 0.642857
-
Convert the decimal to a percentage: Multiply the decimal by 100. 0.642857 x 100 ≈ 64.29%
Therefore, 9 out of 14 is approximately 64.29%. Rounding the percentage to one decimal place is generally sufficient for most practical applications.
Understanding Ratios and Proportions
The concept of "9 out of 14" extends beyond a simple percentage calculation. It represents a ratio, a comparison between two quantities. Understanding ratios is crucial for comprehending proportions. A proportion is a statement that two ratios are equal. For instance:
9/14 = x/100
Solving for 'x' in this proportion provides the percentage equivalent (x ≈ 64.29). This method provides an alternative approach to calculating the percentage.
Real-World Applications: Where Does This Calculation Appear?
The "9 out of 14" scenario, and the principles of ratios and percentages, apply to a wide variety of situations:
-
Academic Performance: Imagine a student answering 9 out of 14 questions correctly on a quiz. Their score would be approximately 64.29%.
-
Survey Results: If 9 out of 14 respondents to a survey favored a particular product, this represents approximately 64.29% approval.
-
Quality Control: In a manufacturing setting, if 9 out of 14 products pass inspection, this indicates a 64.29% success rate, potentially highlighting areas for improvement.
-
Sports Statistics: A basketball player making 9 out of 14 free throws has a free-throw percentage of approximately 64.29%.
-
Financial Analysis: If a company's stock price increases by 9 points out of a total increase of 14 points across a particular period, this is 64.29% of the total growth.
These are just a few examples; the application of percentage calculations based on ratios is virtually limitless.
Beyond the Numbers: Interpreting the Results
While the numerical calculation is important, interpreting the results within the given context is crucial. A 64.29% success rate, for example, might be considered high in one context (e.g., passing a difficult exam) and low in another (e.g., product defect rate). Therefore, always consider the surrounding circumstances when analyzing the significance of a percentage.
Addressing Common Misconceptions
Several misunderstandings frequently arise when working with percentages:
-
Confusing Fractions and Percentages: It's crucial to understand that a fraction represents a part of a whole, and a percentage is simply that fraction expressed as a proportion of 100.
-
Rounding Errors: When working with decimals, rounding can introduce small errors. It's essential to be aware of potential inaccuracies caused by rounding, especially when dealing with multiple calculations.
-
Incorrect Calculation Methods: Always ensure you use the correct formula for converting ratios to percentages to avoid mistakes.
Expanding the Understanding: Proportions and Scaling
The ratio 9/14 can be used to solve proportion problems. For instance:
If 9 out of 14 students in a class prefer apples, and the class has 28 students, how many prefer apples?
We set up a proportion: 9/14 = x/28
Solving for 'x', we get x = 18. Therefore, 18 students in the larger class prefer apples. This demonstrates the use of ratios and proportions in scaling problems.
Advanced Applications: Statistical Analysis
In statistics, ratios and percentages are frequently used to represent frequencies, probabilities, and relative proportions within data sets. Understanding ratios is fundamental to interpreting statistical results and making informed conclusions.
For example, calculating the percentage of successful outcomes in an experiment, analyzing the proportion of different age groups within a population, or assessing the likelihood of an event occurring all involve utilizing ratios and percentages.
Frequently Asked Questions (FAQ)
Q: What if I have a different ratio, like 5 out of 12? How do I calculate the percentage?
A: Follow the same steps outlined above:
- Express as a fraction: 5/12
- Convert to a decimal: 5 ÷ 12 ≈ 0.4167
- Convert to a percentage: 0.4167 x 100 ≈ 41.67%
Q: Is there a quicker way to calculate percentages?
A: While the step-by-step method is clear and ensures accuracy, some calculators have a percentage function that directly converts fractions or decimals to percentages. You can also use online percentage calculators for convenience.
Q: What if the numbers are larger, such as 900 out of 1400?
A: The process remains the same. 900/1400 ≈ 0.6429, which is approximately 64.29%. Notice that the percentage remains consistent, regardless of the scale of the numbers. This highlights the fundamental nature of ratios and their percentage equivalents.
Q: Why is it important to understand percentages and ratios?
A: Percentages and ratios are essential for interpreting data, solving problems, making comparisons, and understanding information presented in various contexts, from academic settings and everyday life to professional fields such as finance, science, and engineering.
Conclusion
Understanding "9 out of 14," and more broadly, the concepts of ratios and percentages, is a critical skill applicable across many areas of life. This article has provided a comprehensive guide to calculating percentages from ratios, exploring real-world applications, addressing common misconceptions, and expanding the understanding to encompass proportions and statistical analysis. By mastering these fundamental concepts, you’ll enhance your ability to analyze data, solve problems, and navigate the numerical world with greater confidence and accuracy. Remember to always consider the context and interpret the results thoughtfully. The ability to translate ratios into percentages and vice-versa is a powerful tool for effective communication and informed decision-making.
Latest Posts
Latest Posts
-
198 Cm How Many Feet
Sep 17, 2025
-
1 74 5 M In Feet
Sep 17, 2025
-
Square Meter To Cubic Meter
Sep 17, 2025
-
3 4 Cup Butter To Sticks
Sep 17, 2025
-
3 4 Cup In Stick Butter
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 9 Out Of 14 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.